方程式の移項のナゾを解いてみよう

Date : 2019-09-07

先日の授業で「方程式の移項」について、丁寧にみていきました。

移項とは、左辺／右辺にある項を反対側へ移動すること。

項を移動するから「移項」と言います。

そして移動する時に「符号を変える」というのがポイントになります。

でも、どうして「符号を変えて移動する」のでしょうか？

もはや、当たり前のように移項を使って計算している中学生や高校生は、いざこう聞かれると、「分かんないけど機械的にそうやってる」「自分が何をしてるのか分かってないけど、とりあえずそういうものだからそうしてる」という人が多いのではないでしょうか？

そこで、移項の正体について、具体的に見ていきましょう！

そもそも方程式とは、生活やビジネスなど、何かしらの日常／社会的な活動の中で、「これを求めたい！」という数（←未知数という）を文字にして、式に表したものです。

それを下のスライドのように、最終的に「x=◯」という形にもっていくことで、欲しかった値を求めようというわけです。

だからポイントは、最初の式を「どうやって最後の形にするか」というところにあります。

それを考える上で、方程式を天秤として見てみると、話が分かりやすくなります。

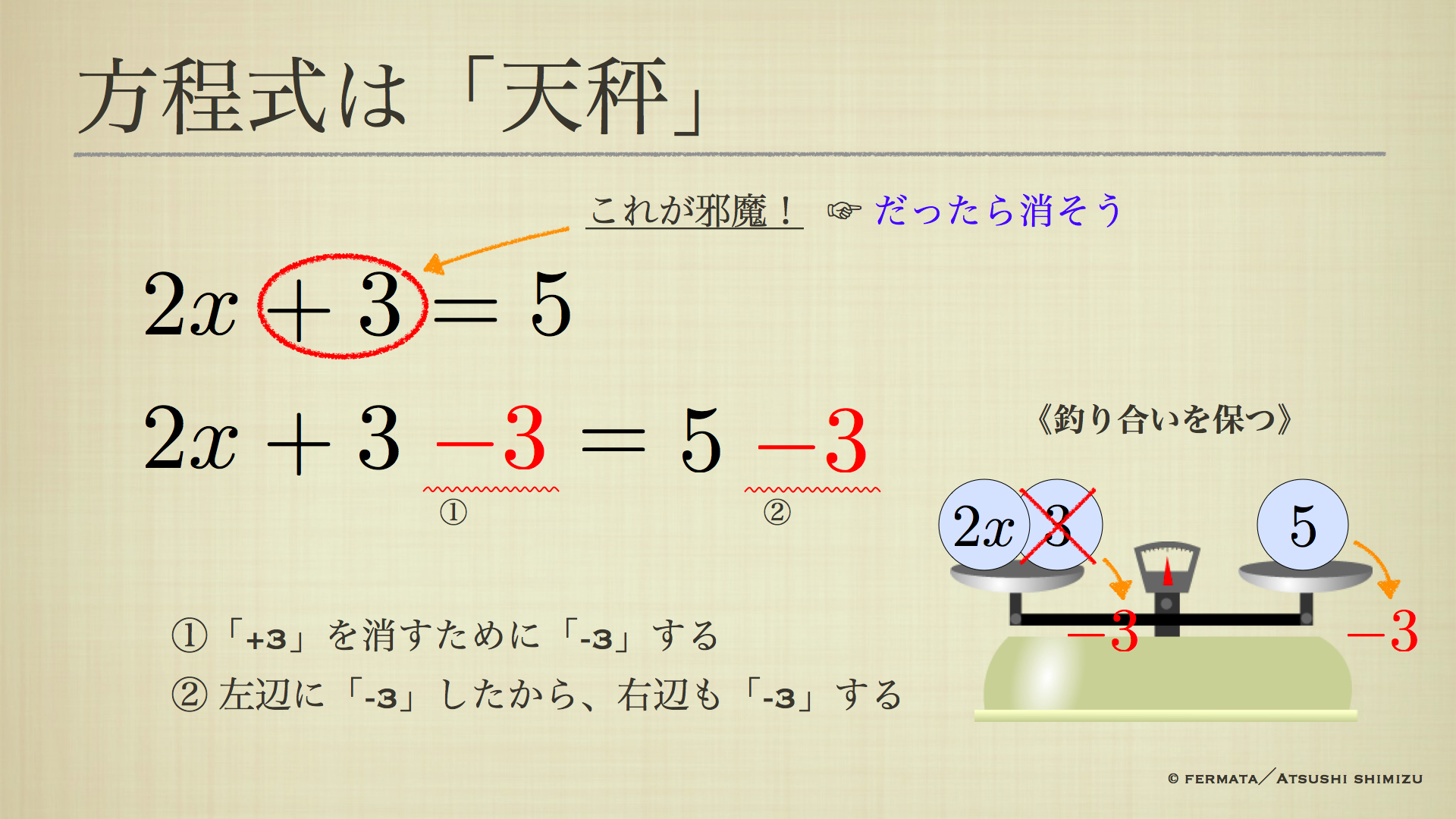
ひとまず方程式の解（未知数の値）は求まりました！

整理すると、ここまでやってきたことは、次の「等式変形」というものがベースになっています。

そして、ここからが本題の「移項」の正体です。

何が見えるか、上のスライドをよ〜く見てみて下さい。

（ヒント：真ん中の式をイメージの中で消して、一番上と下の式をよく見る。）

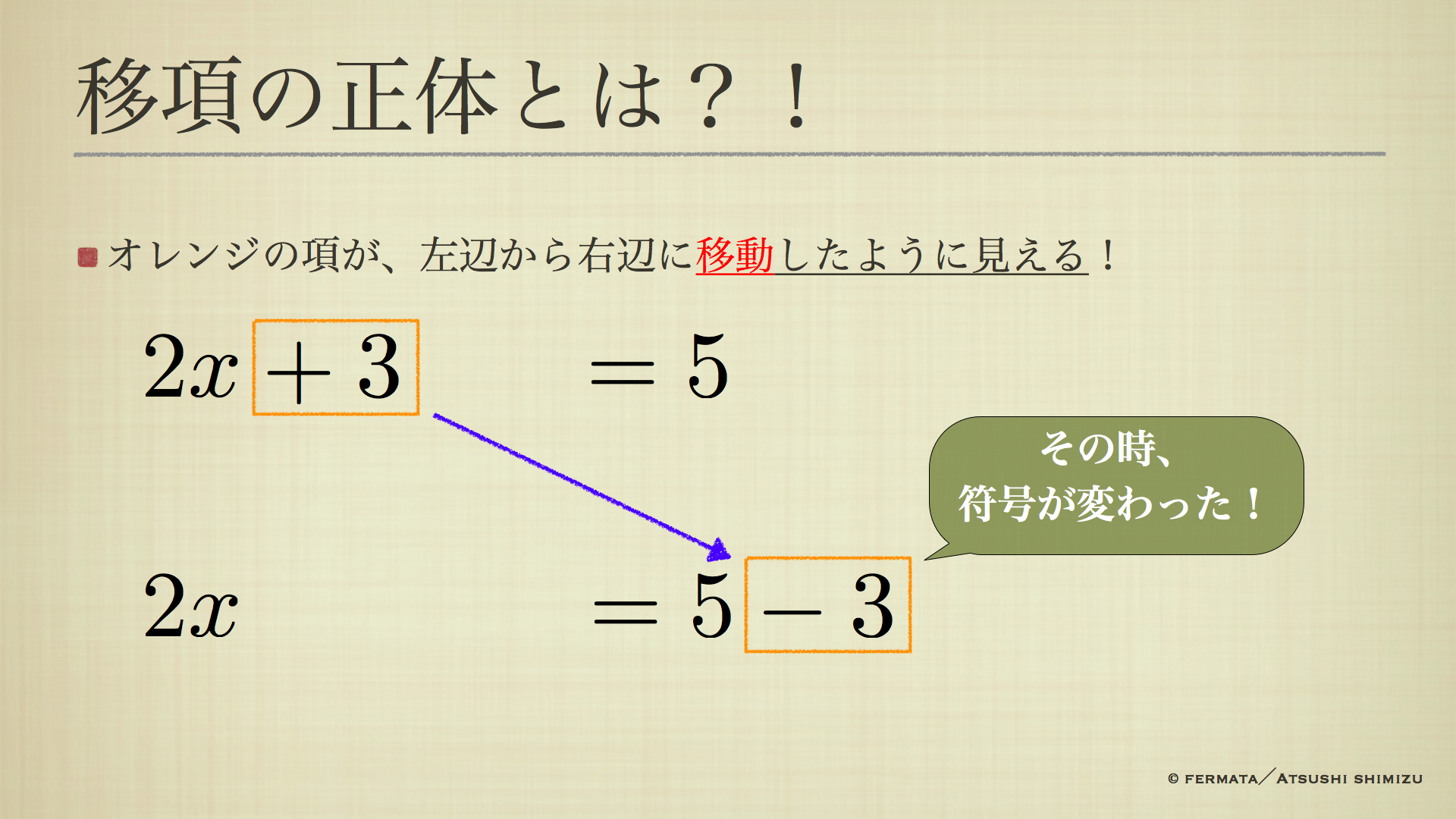
方程式の移項とは、実は等式変形のショートカットだったということが分かりました。

一番最初の式「2x+3=5」を、最後の「x=1」という形にもっていくのには、本当はいくつかの段階を踏んで式変形をしています。でも、方程式を扱うのに、毎回毎回そんなことをしていたら、回りくどいし面倒くさいわけです。

だったら、結果だけ見ると「項が符号が変わって反対に移動している」ように見えるわけだから、これからは方程式の計算・処理は、これで済ませちゃおう！ということです。

移項は、いわば「思考の節約」と言えるわけです。

さて、これで移項の正体がはっきりしたわけですが、ここからは「おまけ」です。

人間、「簡単・速い・便利」だからといってショートカットをしているとどうなるでしょうか…

今回みてきた「思考のショートカット」は、実は日頃から色々なところでやっていたということです。

特に、算数・数学の世界で「公式」と呼ばれるようなものは、すべてこの思考のショートカットと捉えることができるわけです。

● 三角形の面積は？

● 分数の割り算はどうやって計算するか？

● ２次方程式の解を求める公式は？

● ある関数を微分するとどうなるか？

● …

すべて思考のショートカットです。

ショートカットと言うからには、本来の道があったわけです。でも、毎回それをやっていると時間がかかってしまうから、得られた結果（＝それが公式になる）を覚えて使いましょう、となる。

それをすることで、計算は速く楽になる。当然、テストなどで高得点を上げるためには、そうした公式を使いこなすことが必要／重要になる。

でも、そこには実は落とし穴があるわけです。公式を使えば使うほど、算数・数学という教科が知らず知らずのうちに「公式を覚えて問題を解く」教科になっていってしまうのです。

なぜ符号を変えて項を移動することが出来るのか分からないままとりあえず移項しているように、「自分が今何をしているのか分からない」ということを心のどこかで感じながらも、なすすべなく問題を解いているということが積み上がっていってしまいます。

でも、こんな風に「実はこれはショートカットをしてたんだよ」ということに気づかせてあげたり、「ショートカット」という物の見方で色々な事例を“串刺し”にすることで、「ああ、全部そういうことだったんだ！」と、これまでやってきたことを見る眼がガラリと変わって、急に視界が晴れるような体験になったりするわけです。

数学を勉強する／指導するにあたって考えるべきことは色々とありますが、このように分かりやすい言葉を使って軽快なタッチで、「1段高い視点を生徒に与える」ことをするだけで、生徒さんの目（＆精神的な眼）は大きく変わります！